Lim 1/x As X Approaches Infinity
bustaman
Nov 28, 2025 · 10 min read
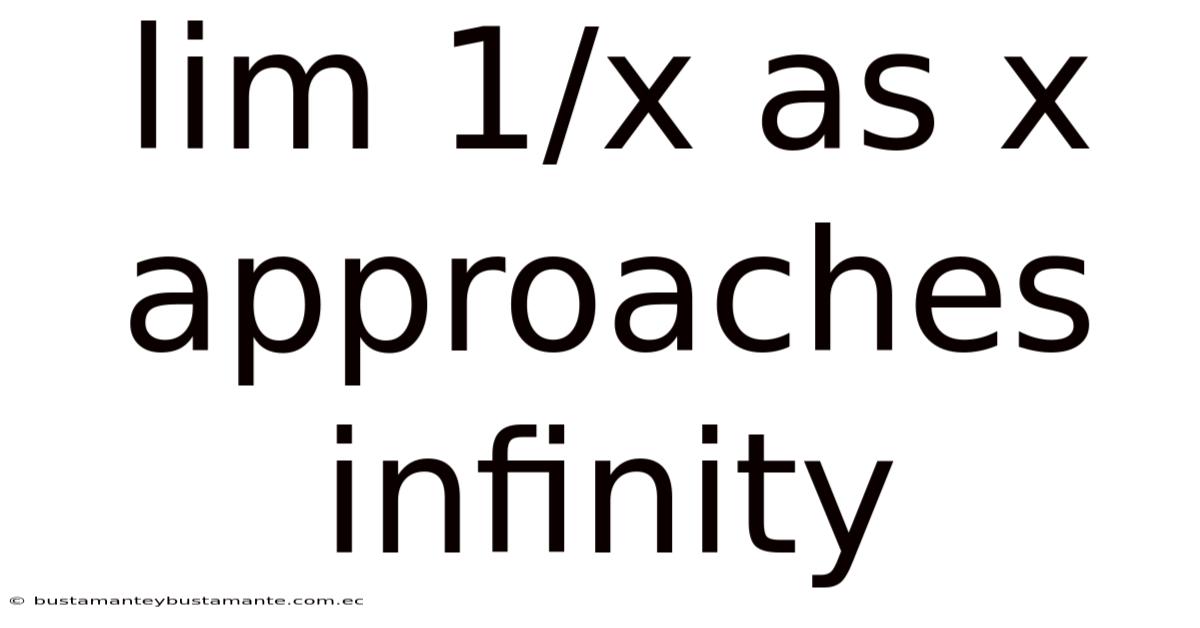
Table of Contents
Imagine you're walking along a straight road that stretches out endlessly. With each step, the distance to the horizon seems to shrink, becoming almost insignificant. You never quite reach the horizon, but you get closer and closer with every stride. That's the essence of understanding limits in calculus, and specifically, the concept of lim 1/x as x approaches infinity.
In mathematics, the concept of a limit allows us to describe the behavior of a function as its argument gets arbitrarily close to a particular value or, in this case, grows without bound. The limit of 1/x as x approaches infinity is a foundational concept in calculus and real analysis, underpinning many advanced topics and applications. Understanding this limit provides essential insights into how functions behave at extreme values, offering a critical tool for analyzing the asymptotic behavior of various mathematical models.
Main Subheading
To truly grasp the concept of lim 1/x as x approaches infinity, it's important to understand the context and background. The limit, denoted mathematically as lim (x→∞) 1/x, asks: "What value does the function 1/x approach as x becomes infinitely large?" This question touches on the heart of calculus, which is concerned with continuous change and the behavior of functions.
Consider the function f(x) = 1/x. As x takes on increasingly large positive values (1, 10, 100, 1000, and so on), the value of 1/x becomes increasingly small (1, 0.1, 0.01, 0.001, and so on). Intuitively, as x becomes infinitely large, 1/x approaches zero. However, it is essential to formalize this intuition using the rigorous definition of a limit to ensure a solid mathematical understanding. This limit is not just a theoretical curiosity; it has profound implications in various fields, including physics, engineering, and computer science, where models often involve analyzing the behavior of systems under extreme conditions.
Comprehensive Overview
The limit of a function describes the value that the function approaches as the input (or argument) approaches a specific point or infinity. In the case of lim (x→∞) 1/x, we're concerned with what happens to the value of the function 1/x as x grows without bound.
Definition of a Limit
Formally, the limit of f(x) as x approaches a is L (written as lim (x→a) f(x) = L) means that for every number ε > 0, there exists a number δ > 0 such that if 0 < |x - a| < δ, then |f(x) - L| < ε. In simpler terms, we can make f(x) as close to L as we want by making x sufficiently close to a.
The Limit as x Approaches Infinity
When dealing with limits at infinity, we modify this definition slightly. The limit of f(x) as x approaches infinity is L (written as lim (x→∞) f(x) = L) means that for every number ε > 0, there exists a number M such that if x > M, then |f(x) - L| < ε. This definition states that we can make f(x) as close to L as we want by choosing a sufficiently large value for x.
Applying the Definition to lim (x→∞) 1/x
For lim (x→∞) 1/x, we want to show that the limit is 0. Let ε > 0 be given. We need to find a number M such that if x > M, then |1/x - 0| < ε. This simplifies to |1/x| < ε. Since x is approaching infinity, we can assume x is positive, so |1/x| = 1/x. Thus, we want to find M such that if x > M, then 1/x < ε.
Solving for x, we get x > 1/ε. So, we can choose M = 1/ε. Then, if x > M, we have x > 1/ε, which implies 1/x < ε. Therefore, |1/x - 0| < ε, satisfying the definition of the limit.
Historical Context
The formalization of limits was a crucial development in the history of calculus. While early mathematicians like Isaac Newton and Gottfried Wilhelm Leibniz developed the basic concepts of calculus in the 17th century, their methods lacked the rigor that modern mathematics demands. It wasn't until the 19th century that mathematicians like Augustin-Louis Cauchy and Karl Weierstrass provided the formal definitions of limits and continuity that we use today.
Cauchy introduced the epsilon-delta definition of a limit, which provided a precise way to define the behavior of functions. Weierstrass further refined these ideas, solidifying the foundation of calculus and real analysis. These developments were essential for resolving paradoxes and inconsistencies that had plagued earlier approaches to calculus.
Significance
Understanding the limit of 1/x as x approaches infinity is not just an academic exercise. It provides a foundation for understanding more complex limits and asymptotic behaviors. For instance, it is used in analyzing the convergence of series, the behavior of algorithms, and the stability of systems.
In physics, this concept is crucial in understanding how forces or fields diminish over distance. In computer science, it helps in analyzing the efficiency of algorithms as the input size grows. In engineering, it is used to design systems that behave predictably under extreme conditions.
Trends and Latest Developments
While the fundamental concept of lim 1/x as x approaches infinity remains unchanged, its applications and interpretations continue to evolve with advancements in various fields. Here are some trends and latest developments:
Computational Mathematics
With the rise of computational mathematics, numerical methods for approximating limits have become increasingly important. These methods are used to estimate the values of limits that are difficult or impossible to compute analytically. Techniques such as Richardson extrapolation and numerical differentiation rely on the understanding of limits to improve accuracy.
Big Data Analysis
In the era of big data, understanding asymptotic behavior is crucial. As datasets grow to enormous sizes, algorithms must be designed to scale efficiently. The limit of 1/x as x approaches infinity provides a basic model for understanding how performance metrics (such as runtime or memory usage) change as the input size increases.
Machine Learning
Machine learning algorithms often involve iterative processes that converge to a solution. The concept of a limit is used to define and analyze the convergence of these algorithms. For example, gradient descent, a common optimization technique, relies on taking small steps towards a minimum. The size of these steps is often determined by a learning rate, which must be chosen carefully to ensure convergence. Understanding limits helps in selecting appropriate learning rates and analyzing the convergence properties of these algorithms.
Quantum Computing
In quantum computing, the behavior of quantum systems is often described by wave functions. Analyzing the asymptotic behavior of these wave functions is essential for understanding the properties of quantum systems. The limit of 1/x as x approaches infinity can serve as a building block for more complex asymptotic analyses in quantum mechanics.
Educational Approaches
Modern educational approaches emphasize a deeper understanding of the underlying concepts rather than rote memorization. Interactive simulations and visualizations are increasingly used to help students grasp the concept of limits. These tools allow students to explore the behavior of functions as x approaches infinity and to see how the limit is approached graphically.
Tips and Expert Advice
Understanding lim 1/x as x approaches infinity is more than just memorizing a result; it's about developing a deep intuition for how functions behave. Here are some practical tips and expert advice to help you master this concept:
Visualize the Function
One of the most effective ways to understand the limit is to visualize the function f(x) = 1/x. Plot the graph of the function and observe what happens as x becomes very large. You'll notice that the graph gets closer and closer to the x-axis (y = 0) but never actually touches it. This visual representation can solidify your understanding of the limit.
Use Numerical Examples
Another helpful technique is to plug in increasingly large values of x and observe the corresponding values of 1/x. For example, try x = 10, 100, 1000, 10000, and so on. You'll see that 1/x becomes smaller and smaller, approaching zero. This numerical experimentation can reinforce your intuition about the limit.
Understand the Epsilon-Delta Definition
While the epsilon-delta definition of a limit can seem abstract, it is essential for a rigorous understanding. Work through examples to see how the definition applies in practice. This will help you develop a deeper appreciation for the precision of calculus.
Relate to Real-World Examples
Try to relate the concept of a limit to real-world situations. For example, consider the decay of a radioactive substance. As time goes on, the amount of the substance decreases, approaching zero. This is an example of a limit in action.
Practice with Variations
Once you understand the basic limit of 1/x as x approaches infinity, try working with variations of the function. For example, consider lim (x→∞) 1/(x^2) or lim (x→∞) 1/(x+1). These variations will help you generalize your understanding and develop problem-solving skills.
Use Technology
Take advantage of technology to explore the concept of limits. Use graphing calculators, computer algebra systems, or online tools to plot functions and compute limits. These tools can help you visualize the behavior of functions and confirm your analytical results.
Seek Feedback
Don't hesitate to ask for help from teachers, professors, or online communities. Explaining your understanding to others and receiving feedback can help you identify gaps in your knowledge and deepen your comprehension.
FAQ
Q: What does it mean for x to approach infinity?
A: When we say that x approaches infinity (x → ∞), it means that x is growing without bound, taking on increasingly large values without any upper limit. It doesn't mean that x is reaching a specific number called "infinity," but rather that it's getting arbitrarily large.
Q: Why is the limit of 1/x as x approaches infinity equal to zero?
A: As x becomes infinitely large, the value of 1/x becomes infinitely small, approaching zero. For example, if x is a million, 1/x is one millionth. If x is a billion, 1/x is one billionth. As x continues to grow, 1/x gets closer and closer to zero.
Q: Is infinity a number?
A: No, infinity is not a number. It is a concept representing a quantity that is without any bound. In the context of limits, we use infinity to describe the behavior of a function as its input grows without limit.
Q: Can a function actually reach its limit?
A: A function does not necessarily have to reach its limit. The limit describes the value that the function approaches as its input approaches a certain value. In the case of 1/x as x approaches infinity, the function gets arbitrarily close to zero but never actually reaches it.
Q: How is the limit of 1/x as x approaches infinity used in real-world applications?
A: This limit is used in various fields, including physics, engineering, and computer science. For example, it can be used to analyze the decay of signals, the stability of systems, and the efficiency of algorithms as input sizes grow.
Conclusion
In summary, lim 1/x as x approaches infinity is a fundamental concept in calculus that illustrates how a function behaves as its input grows without bound. The limit is equal to zero, meaning that as x becomes infinitely large, the value of 1/x approaches zero. This concept is not just a theoretical curiosity; it has practical applications in various fields, including physics, engineering, computer science, and data analysis.
By understanding the formal definition of a limit, visualizing the function, and working through examples, you can develop a solid understanding of this essential concept. Embrace the challenge, explore the applications, and deepen your understanding of the behavior of functions.
Now that you have a comprehensive understanding of lim 1/x as x approaches infinity, take the next step: try applying this knowledge to solve related problems, explore more advanced calculus concepts, and share your insights with others. Leave a comment below with your questions or insights, and let's continue the discussion!
Latest Posts
Latest Posts
-
What Is The Work Of Energy
Nov 28, 2025
-
Best Way To Learn Multiplication Tables
Nov 28, 2025
-
The Process By Which Rna Is Made From Dna
Nov 28, 2025
-
Where Is The Lower Pole Of The Kidney
Nov 28, 2025
-
Which Colony Was Not Represented In The First Continental Congress
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about Lim 1/x As X Approaches Infinity . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.