Divide 100 By 1 2 And Add 100
bustaman
Nov 23, 2025 · 8 min read
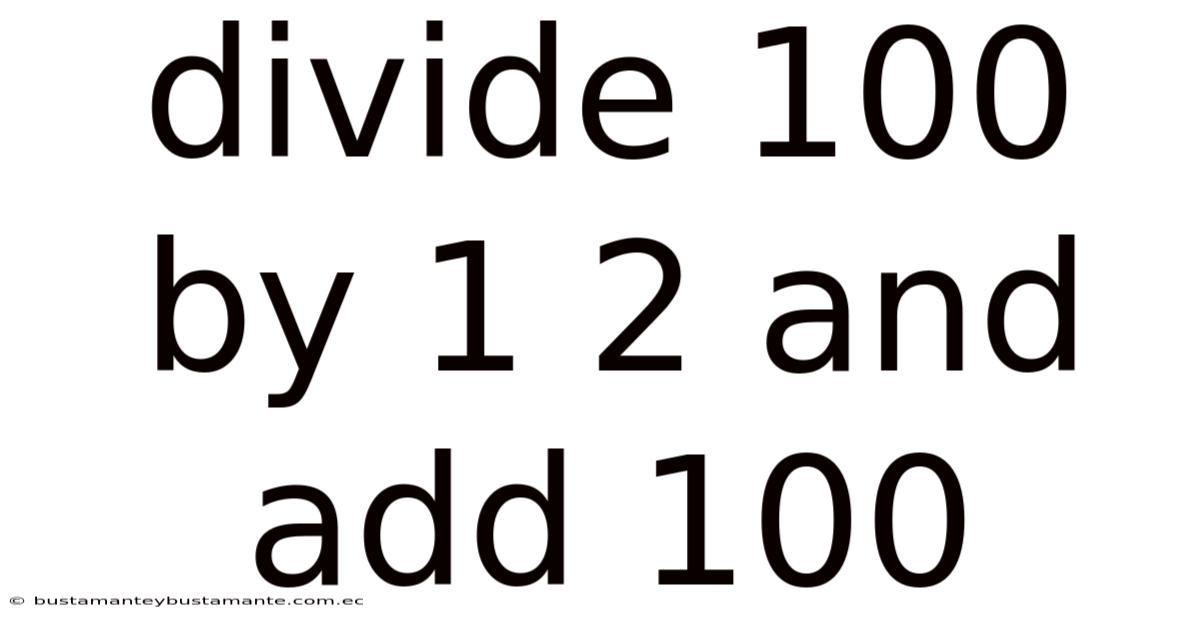
Table of Contents
Imagine you're at a lively math party, and someone throws out the challenge: "Divide 100 by 1/2 and add 100!" It sounds straightforward, but watch out—this is where many stumble. It's a classic brain teaser that plays on how we intuitively approach mathematical problems. So, how do we solve it, and what's the trick to getting it right every time?
Let’s walk through this intriguing math problem step-by-step. Understanding the correct method not only helps you solve this particular question but also sharpens your overall mathematical reasoning. Along the way, we'll explore why it often trips people up and how to avoid common mistakes. So, grab your mental calculator, and let’s dive into the solution and some fun mathematical explorations.
The Intriguing Problem: Divide 100 by 1/2 and Add 100
At first glance, the problem "Divide 100 by 1/2 and add 100" appears simple. However, its phrasing often leads to incorrect answers. The key lies in understanding the order of operations and the impact of dividing by a fraction. Many people quickly assume that dividing 100 by 1/2 means dividing 100 in half, but that's where the confusion begins.
This mathematical puzzle is more than just a simple calculation; it’s a test of how well we understand fundamental arithmetic principles. Dividing by a fraction can sometimes feel counterintuitive, which is why this problem is a popular brain teaser. It highlights the importance of carefully reading and correctly interpreting mathematical expressions to arrive at the right solution. By dissecting this problem, we reinforce our basic math skills and improve our ability to tackle similar challenges in the future.
Comprehensive Overview of the Math Problem
To truly understand the problem, let's break down each component and the underlying mathematical concepts.
Understanding Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It involves splitting a number into equal parts. When we say "100 divided by 2," we mean splitting 100 into two equal parts, resulting in 50. However, division takes on a different dimension when dealing with fractions.
The Peculiarity of Dividing by Fractions
Dividing by a fraction might seem odd at first. Instead of splitting a number into smaller parts, dividing by a fraction actually increases the number. This is because dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is obtained by swapping the numerator and the denominator. For example, the reciprocal of 1/2 is 2/1.
The Reciprocal Relationship
When you divide a number by a fraction, you're essentially asking how many times that fraction fits into the number. For instance, when we divide 100 by 1/2, we’re asking how many halves are there in 100. Since each whole number contains two halves, 100 contains 200 halves. This is why dividing by a fraction results in a larger number.
Order of Operations
In mathematics, the order of operations is a set of rules that dictate the sequence in which operations should be performed in an expression. The acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) is often used to remember this order. Multiplication and division are performed from left to right, as are addition and subtraction. In our problem, "Divide 100 by 1/2 and add 100," division comes before addition.
The Correct Solution
Now that we've covered the essential concepts, let's solve the problem correctly:
- Divide 100 by 1/2: 100 ÷ (1/2) = 100 * 2 = 200
- Add 100 to the result: 200 + 100 = 300
Therefore, the correct answer is 300.
Trends and Latest Developments in Mathematical Education
In recent years, there has been a shift in mathematical education towards emphasizing conceptual understanding over rote memorization. Educators are increasingly focusing on teaching students the "why" behind mathematical operations, rather than just the "how." This approach aims to foster a deeper, more intuitive understanding of mathematics, making it easier for students to apply their knowledge to real-world problems.
Interactive Learning
One significant trend is the use of interactive learning tools and technologies in mathematics education. These tools range from online simulations and games to interactive whiteboards and educational apps. Interactive learning can make mathematics more engaging and accessible for students, helping them visualize abstract concepts and practice problem-solving in a dynamic environment.
Problem-Solving and Critical Thinking
Another important development is the emphasis on problem-solving and critical thinking skills. Instead of focusing solely on performing calculations, students are encouraged to analyze problems, develop strategies, and justify their solutions. This approach helps students develop a deeper understanding of mathematical concepts and their applications.
Real-World Applications
Connecting mathematics to real-world applications is also gaining prominence. By showing students how mathematical concepts are used in various fields, such as science, engineering, and finance, educators can make mathematics more relevant and engaging. Real-world examples help students see the value of mathematics and motivate them to learn more.
Personalized Learning
Personalized learning approaches are also on the rise, leveraging technology to tailor instruction to individual student needs. Adaptive learning platforms can assess a student's strengths and weaknesses and provide customized lessons and practice exercises. This ensures that each student receives the support they need to succeed, regardless of their background or learning style.
Tips and Expert Advice for Solving Mathematical Problems
To enhance your problem-solving skills in mathematics, consider the following tips and expert advice:
Read Carefully and Understand the Problem
The first and most crucial step is to read the problem carefully and ensure you understand what it is asking. Pay attention to the wording, any specific instructions, and the context of the problem. Misinterpreting the problem is a common mistake that can lead to incorrect solutions.
Break Down Complex Problems
Complex problems can be overwhelming, but breaking them down into smaller, more manageable steps can make them easier to solve. Identify the different components of the problem and address each one individually. This approach can help you stay organized and avoid getting bogged down by the complexity of the problem.
Use Visual Aids
Visual aids such as diagrams, charts, and graphs can be incredibly helpful in visualizing mathematical concepts and relationships. Drawing a diagram can help you see the problem from a different perspective and identify patterns or relationships that might not be immediately apparent.
Practice Regularly
Like any skill, mathematical problem-solving improves with practice. Make it a habit to practice regularly, working through a variety of problems to reinforce your understanding of different concepts and techniques. The more you practice, the more confident and proficient you will become.
Review Mistakes and Learn from Them
Everyone makes mistakes, but the key is to learn from them. When you make a mistake, take the time to understand why you made it and how to avoid making the same mistake in the future. Reviewing your mistakes can help you identify areas where you need to improve and strengthen your understanding of the material.
Seek Help When Needed
Don't be afraid to ask for help when you're struggling with a problem. Whether it's a teacher, tutor, or classmate, seeking assistance can provide you with new insights and perspectives. Explaining the problem to someone else can also help you clarify your own understanding and identify areas where you need further clarification.
FAQ About Mathematical Problem-Solving
Here are some frequently asked questions about mathematical problem-solving:
Q: Why is it important to follow the order of operations? A: Following the order of operations ensures that mathematical expressions are evaluated consistently, leading to a unique and correct answer. Without a standard order, different people could interpret the same expression in different ways, resulting in conflicting answers.
Q: How can I improve my mental math skills? A: Improving your mental math skills requires practice and familiarity with basic arithmetic operations. Try practicing mental calculations regularly, breaking down complex problems into simpler steps, and using techniques like estimation and approximation.
Q: What are some common mistakes to avoid in math problems? A: Common mistakes include misinterpreting the problem, neglecting the order of operations, making arithmetic errors, and overlooking important details. Double-checking your work and paying attention to detail can help you avoid these mistakes.
Q: How can I make math more enjoyable? A: Making math more enjoyable involves finding ways to connect it to your interests and making it more engaging. Try exploring math-related games, puzzles, and activities, or looking for real-world applications of math that you find interesting.
Q: What is the role of technology in learning math? A: Technology can play a significant role in learning math by providing access to interactive learning tools, simulations, and personalized instruction. Technology can also help students visualize concepts, practice problem-solving, and receive immediate feedback on their progress.
Conclusion
So, to definitively answer the challenge: Divide 100 by 1/2 and add 100. The correct answer is 300. This problem perfectly illustrates how critical it is to pay close attention to detail and accurately apply the order of operations. Remember, dividing by a fraction is the same as multiplying by its reciprocal, which often surprises those who approach the problem too quickly.
To further boost your math skills, make practice a regular part of your routine. Explore different types of problems, challenge yourself, and don't hesitate to seek help when you need it. Now that you've mastered this tricky math puzzle, why not share it with your friends and see if they can solve it too? Engage in mathematical discussions, explore new concepts, and continue to develop your problem-solving abilities. Keep challenging yourself, and you'll find that math can be both engaging and rewarding.
Latest Posts
Latest Posts
-
What Is The Unit To Measure Sound
Nov 23, 2025
-
How To Write Examples In A Sentence
Nov 23, 2025
-
The Birth Of Venus Botticelli Analysis
Nov 23, 2025
-
How Many Pounds Are In 32 Oz
Nov 23, 2025
-
Map Of The Ancient Near East
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about Divide 100 By 1 2 And Add 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.